1  2  3  4  5  6  7  8  Contents

集合

        將一些有明確性質的東西看成一體，就形成一個集合，例如：{所有會飛的動物}, {所有能被5整除的正整數}, {所有法國或德國進口的跑車} 等都是集合。至於沒有元素的集合，我們特別稱之為空集合（empty set），用符號表示，如 {有四個邊的三角形}, {會下蛋的公雞} 都是空集合，而且，我們認為空集合只有一個，也就是說 {有四個邊的三角形} = {會下蛋的公雞} = 。

        集合常以大寫英文字母表示，如：A, B…，而裡頭的元素則以小寫英文字母表示，如：a, b……。若要說x是集合A中的元素，我們記做 xA；否則記做xA。另外，我們會將元素以大括號 { } 括起來以表示它們在一個集合中。

        我們常常把要討論的集合放在某個足夠大的集合中，稱為宇集（universal set），用符號U來表示。假設B集合含有A集合的所有元素，則稱A為B的子集（subset），以AB表示。

        上一個故事中我們談到「如果戴珠寶就是傻瓜」，這個敘述也可以說成「戴珠寶的人都是傻瓜」，其實說得更清楚一點應該是：「所有戴珠寶的人都是傻瓜。」
「所有戴珠寶的人都是傻瓜。」這個敘述中，牽涉了兩個集合：

A = {所有戴珠寶的人}
B = {所有的傻瓜}

「所有戴珠寶的人都是傻瓜」若為真，則表示AB。這也就是為什麼我們稱「若p則q」為蘊含命題。

       不論在口語或數學上的敘述，常常包含了「所有」或「有些」這兩類的述詞。我們看看下面這四種型式的命題：

「所有的A都是B」、「有些A是B」、「所有的A都不是B」和「有些的A不是B」。我們將這四種命題各舉一例如下：

1. 所有本班的同學都喜歡數學。

2. 有些本班的同學喜歡數學。

3. 所有本班的同學都不喜歡數學。

4. 有些本班的同學不喜歡數學。

上面這些例子中，第一、第三個敘述中「所有」兩個字是普遍性的，叫做全稱（universal）命題。另外兩個敘述中的「有些」兩個字是存在性而非普遍性的，叫做特稱（existential）命題。而前兩個敘述是肯定的，後兩個敘述是否定的。所以這四個類型的敘述就分別稱為：全稱肯定命題，特稱肯定命題，全稱否定命題和特稱否定命題。

　

        1761年，瑞士數學家尤拉（Leonhard Euler, 1707-83）以圖形來描述這四類命題，也就是所謂的尤拉圓（Euler circles）。

 

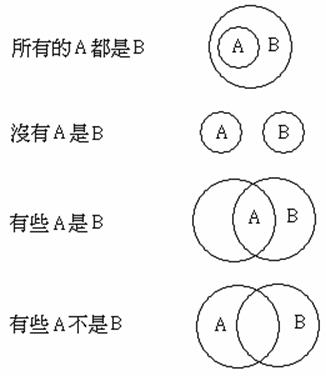
        1881年英國數學家范恩（John Venn, 1834-1923）出版的《符號邏輯》（Symbolic Logic）書中，改良了尤拉的原始想法，創造出知名的范氏圖（Venn diagram）。范氏圖的方法是處理牽涉到命題變數的邏輯論證。各個命題變數分別以互相重疊的圓來表示，而各個區域則代表特定的邏輯敘述。舉例來說：

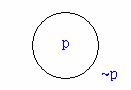
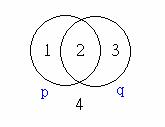
(1)   若p為一命題，則下圖中圓內之區域表示p，圓外之區域表示 ~p。

 

(2)   若p, q為兩個命題變數，如下圖左圓為p，右圓為q，則區域2表示pq，區域1, 2, 3表示pq，而區域1, 3, 4是指 ~(pq)，區域4則是 ~(pq)。

(3)   如果論證中牽涉到三個命題變數p, q, r，「范氏圖」則以如下圖形表示：

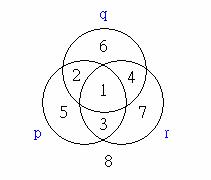
其中pq所指的就是區域1和區域2，而 (pq)r指的是區域1, 2, 3, 4以及7；p(qr) 則是區域1, 2, 3，與 (pq)r不同。觀察上面的范氏圖，我們可以了解：表示p(qr) 的區域是1, 2, 3；而表示 (pq), (pr) 的區域分別是1, 2及1, 3，所以 (pq)(pr) 的區域也是1, 2, 3。這說明了分配律

p(qr)  (pq)(pr)

同理，我們也可看出另一項分配律

p(qr)  (pq)(pr)

　

       范氏圖為邏輯學家提供了一個展示物件類別的方法，這個方法在現代的邏輯、電腦科學、語言學、認知科學、決策理論、工程及其他學科裡仍被廣泛使用。