我們所在的世界瞬息萬變,然而多數都有規律可循。太陽昇起落下,潮起、潮落,動物在陸地上奔馳、在空中飛翔、在水中悠游,植物生長,人口的增長等等。如何能描述並了解這些變化?人們花了兩千多年的努力才發展出有效的數學工具來完成這件事。而這其中關鍵的一大步便是微積分(Calculus)的產生。Calculus——原本是拉丁文,意思是小石子。早期人們拿小石子來計數、做計算,因此 Calculus 這個字代表的意思可以解釋成計算工具。
在微積分發展之前的數學只能做有限步驟的計算,所能處理的問題是單純有簡單規律的。舉例來說:大家都學過:速度=
,而這裡所指的速度是平均速度;若是等速運動,那麼任何時間的速度都相同都等於平均速度。因此,我們也就稱之為速度。假設有一輛車以固定的速度從台北行駛到新竹(約 100 公里)花了一小時,我們知道車速是每小時 100 公里。然而,在現實生活中上述的情形是不可能存在的,姑且不論車行路況(紅綠燈、塞車、……),車子須要加速才能從靜止狀態起動,這段時間內的車速是不可能維持固定的。儀表板上計速器的指針隨著踩油門的節奏轉動,指針所指的數字到底是什麼意思?我們如何能正確地得出任一時間車子的速度呢?
另外一個典型的例子就是面積的計算。我們定義一個邊長為 1 單位的正方形面積為 1 平方單位,如下圖:
那麼當我們要求某塊區域的面積時,就必須算算看該區域可以分成幾個這樣的單位正方形。
若某長方形的長為 4 單位,寬為 2 單位,則我們可以將長方形先縱切成 4 個部分,下圖以 4 種顏色表示:
每一部分又可以橫切為 2 部分:
所以這個長方形的面積 = 2 + 2 + 2 + 2 = 4 × 2 = 8。
正如同大家所熟悉的,長方形面積 = 長 × 寬。
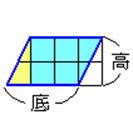
而對於下面的藍色平行四邊形而言,只要將它左邊的黃色三角形移至右邊,就會變成一個紅色長方形,於是我們知道它的面積就是底 × 高。
至於三角形,觀察下圖我們發現左邊黃色三角形的面積恰好是黃色矩形的二分之一,而右邊的藍色三角形也是藍色矩形的一半大,因此,三角形的面積等於底乘高的一半。
然而圓的面積呢?
有人說是「3 × 半徑的平方」。
有人說是「3.14 × 半徑的平方」。
有人說是「圓周率 × 半徑的平方」。
然而,圓周率又是什麼呢? 等於 3? 等於 3.14?或是等於 3.14159.....?這個 「.....」又是什麼?