假設 f 與 g 在 x 的微分都存在，
（i） 則對於任意實數 a, b，a f + b g 在 x 的微分存在，而且
( a f + b g)'(x) = a f '(x) + b g'(x)
（ii） 則 f g 在 x 的微分存在，而且 ( f g)'(x) = f '(x) g(x) + f (x) g'(x)
（iii） 若 g'(x) 不為0，則在 x 的微分存在，而且
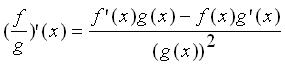
有了上面的法則，許多函數的微分就十分容易計算了。
例如：若要知道 h(x) = 2 x2 + 3 x 的微分，我們可以考慮 f (x) = x2, g(x) = 3 x。這兩個函數的微分分别是 f '(x)= 2 x, g'(x) = 3（g(x) = 3 x 就是之前所提過的等速度運動，速率為 g'(x) = 3）。
由於
h(x) = 2 x2 + 3 x = (2 f + g)(x) = 2 f (x) + g(x)
因此，
h'(x) = ( 2 f + g)'(x) = 2 f '(x) + g'(x) = 4 x + 3
又如：若要知道 h(x) = x3 的微分，我們可以考慮 f (x) = x2, g(x) = x。因為
h(x) = x3 = x2 x = f (x) g(x)= ( f g)(x)，
因此，
h'(x) = ( f g)'(x) = f '(x) g(x) + f (x) g'(x) = (2x) (x) + (x2)(1) = 2 x2 + x2 = 3 x2。
如上例，用數學歸納法我們可以證得
若 f (x) = xn，其中 n 為正整數，則 f '(x) = n xn-1。
若 f (x) = xp，其中 p 為整數時又如何呢？
當 p = 0 時，f (x) = x0 = 1 為常數，表示無論 x 如何變化 f (x) 永遠是 1，不會增加也不會減少，所以 f '(x) = 0。
當
p
< 0 時，只要
，我們可以將
f (x) = xp
視為兩個函數相除，分子為 1，分母為
xq，即
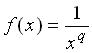，其中
q
= – p > 0。則利用除法的微分公式，我們可以得到
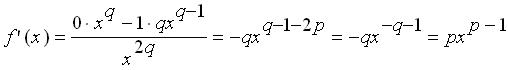
因此，我們得到
若 f (x) = xp，其中 p 為整數，則 f '(x) = p xp-1。
函數的微分可以告訴我們函數的變化情形：概括地說，如果在某個區間函數的微分值均為正數，則在該區間函數為遞增（輸入值 x 愈大，輸出值 f (x) 也愈大）；如果在某個區間函數的微分值均為負數，則在該區間函數為遞減（輸入值 x 愈大，輸出值 f (x) 愈小）。若在某個點函數的微分值為零，則表示函數在該點可能有局部的極大或極小值。
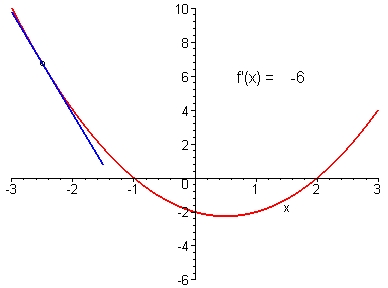
例如：f
(x) = x2，f
'(x)
= 2x。
當 x > 0，f '(x) 大於 0，這表示 f (x) = x2 在右半平面會一直遞增。
當 x < 0，f '(x) 小於 0，這告訴我們 f (x) 在左半平面會一直遞減。
當 x = 0，f '(x) 等於 0。
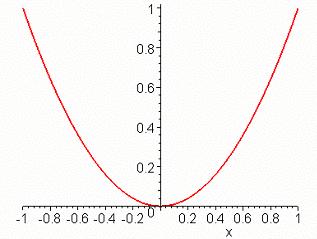
讓我們看一看，當 x < 0 時，f (x) 一直遞減，也就是隨著 x 值愈來愈大（愈來愈接近 0），f (x) 會愈來愈小，所以 f (0) 比左半平面的任何一個 f (x) 都小；再看看右半平面，f (x) 一直遞增，即 x 值愈大，f (x) 也愈大，所以對於所有大於 0 的 x，f (x) 都比 f (0) 大。由此可見，f (0) 是一個極小值，也是一個最小值。而微分學的典型應用即是 最大最小問題。
如果我們從長為 30 吋且寬為 16 吋之薄紙板的四個角截去大小相等的正方形，並將各邊向上折疊以做成開口盒子。若要使盒子的體積為最大，應該如何截去四個角呢？
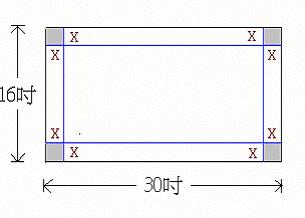
若 x = 所截去正方形的邊長（以吋計），則我們從每一個角截去邊長為 x 的正方形所做出盒子的體積為 (30 – 2x )(16 – 2x)x = 480x – 92x2 + 4x3（立方公吋）。
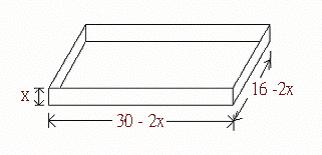
因此我們得到一個盒子的體積函數
V(x) = (30 – 2x )(16 – 2x)x = 480x – 92x2 + 4x3
因上式中的變數
x
代表長度而且紙板的寬為
16
吋，我們不可能截去邊長大於
8
吋的正方形，所以
x
必須滿足 
。因此，這個問題便成了求在
[0, 8]中的
x
值使得
V(x)
為極大，由於
可知在
[0, 8]中使得
V
'(x)
= 0
的
x
只有 
。
觀察下表：
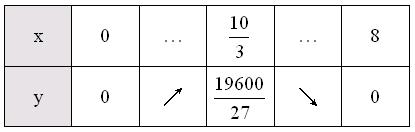
我們得知當截去邊長為
吋的正方形時，盒子有最大的體積
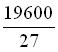立方吋。