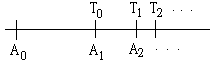
大約出生於西元前 480 年的希臘哲學家季諾（Zeno）曾經提出幾 則似是而非的辨證，其中一個是著名的「阿奇里斯和陸龜賽跑」（Achilles and the tortoise）。季諾證明行動矯捷的阿奇里斯永遠趕不上一隻搶先起步的笨重陸龜。因為如下圖，假設開始時阿奇里斯的位置在 A0，陸龜則在前面的 T0 處。等阿奇里斯趕到 T0 處時，陸龜雖然跑得慢，卻並非原地踏步，所以這時已經跑到前面的 T1 處了；同樣的道理，當阿奇里斯趕到 T1 處時，陸龜又已經跑到前頭的 T2 處了。如此繼續下去，雖然阿奇里斯愈趕愈近，但總是落後一點點，永遠無法追上陸龜。
每個人都知道，在現實世界中阿奇里斯在一小段距離後就能超過陸龜；但是上述季諾的推演似乎也無懈可擊，為什麼會出現如此矛盾的結果呢？“無限”就是癥結所在。 我們可以把實際情況簡化如下：「假設阿奇里斯每秒只能跑 1 公尺，陸龜每秒可以跑 1/2 公尺。比賽開始時，陸龜的起點在阿奇里斯前面 1/2 公尺處。」
我們知道經過 1 秒後，陸龜跑了 1/2 公尺，阿奇里斯跑了 1 公尺，這時阿奇里斯就追上陸龜了。
照季諾的說法，阿奇里斯要先花 1/2 秒跑到陸龜一開始的位置 ---- 1/2 公尺處，但這時陸龜也向前跑了 1/4 公尺，所以阿奇里斯又得花 1/4 秒去跑到新位置，同時陸龜也又向前跑了 1/8 公尺。以此類推，阿奇里斯得向前跑 1/2 + 1/4 + 1/8 + … 公尺去追陸龜。
綜合以上兩種說法我們不難發現： 1/2 + 1/4 + 1/8 + … 公尺這無限多小段距離的總和其實是一段有限的距離 ---- 1 公尺；同樣地，阿奇里斯追陸龜所花的時間 1/2 + 1/4 + 1/8 + … 秒，這無限多段時間的總和也只是短短的 1 秒鐘罷了。
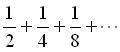等於
1，那麼現在考慮下面這個問題
，答案又會是什麼呢？
1 – 1 + 1 – 1 + 1 – 1 + …… = ？
“無窮大”、“無窮小”所造成的困擾，許多年之後，經過數學家高斯（Gauss）及魏爾斯查士（Karl Weirstrass）等人的努力，引入極限的觀念才得以解決。