1  2  3  4  5  6  7  8  9   Contents

圓面積與圓周率 

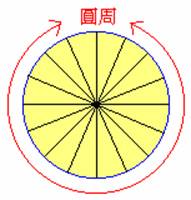
        我們若將圓切成許多相同大小的扇形，再將這些扇形展開，而空隔處也填入相同大小的扇形，如下圖，則我們就得到一個近似平行四邊形的區域。

  

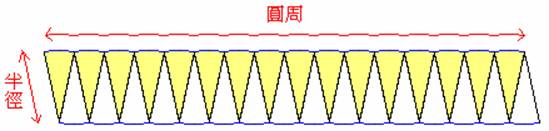
不難看出這塊區域的面積會是圓面積的 2 倍。如果我們將圓分成更多更細更窄的扇形，那麼這塊區域就會愈來愈像下面這個矩形： 

於是我們得到下面的公式：

       2 × 圓面積 = 圓周 × 半徑 = 2π r × r 
ð     圓面積 = π r²

        你知道埃及人如何計算圓周率嗎？ 

      

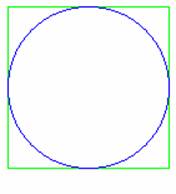
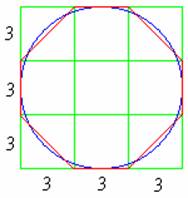
如上圖，將圓的外切正方形等分成九個小方格。若令圓的直徑為 9 單位，那麼外切正方形的邊長也是 9 單位，而每個小方格的邊長則是 3 單位，於是我們知道每個小方格的面積是 3 × 3 = 9 平方單位。接著沿小方格畫一個八邊形，如上圖紅線的部分，埃及人就是用這個八邊形的面積來估計圓面積的。

　

 

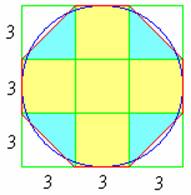
        觀察上面的圖形，我們知道這個八邊形是由 5 個黃色小方格與 4 個藍色三角形所組成，而每個藍色三角形的面積又是小方格的一半，所以總共是 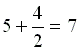個小方格。於是我們得到八邊形面積 = 7 × 9 = 63，也就是近似的圓面積。又由公式知道圓面積應該是 π r²，那麼 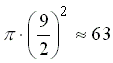。為了方便計算，我們可以再用平方數 64 來取代 63。於是

埃及人所計算出來的圓周率比實際值要大了一點，他們的誤差是來自於以八邊形面積來估計圓面積，以及後來又以 64 取代 63。

 

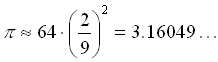
        阿基米德用圓的內接正 n 邊形的周長來計算圓周率，他算的圓周率介於 及 之間；三國時的劉徽則利用圓的內接正 n 邊形的面積來計算圓周率，他得出的近似值為 3.14159。他們都找出圓的內接正 2n 邊形與圓的內接正 n 邊形周長 （或面積）的關係式，從內接正四邊形或正六邊形出發，讓邊數一再倍增而求得更精確的圓周率估計值，阿基米德稱這種方法為「窮盡法」(Method of Exhaustion)。南北朝的祖沖之居然利用這種方法算到 16384 ( 4 × 2¹² ) 邊，而得到圓周率介於 3.1415926 及 3.1415927 之間，準確至小數以下七位，這個紀錄維持了近千年才被打破！！！