1  2  3  4  5  6  7  8  9   Contents

圓周長與圓周率 

圓會因半徑不同而有大有小，但圓周長與直徑的比值卻不會因圓的大小而改變；這個比值就是所謂的圓周率，通常以希臘字母 π 表示。
 
        為什麼圓周長和直徑的比值是常數呢？西元前四世紀，希臘的數學家尤多瑟斯（Eudoxus）給了一個十分嚴謹的證明，其中主要的想法 是 

「當 n（n 為正整數）愈來愈大時，圓的內接正 n 邊形就會“ 變成 ”圓。」

　

 

 

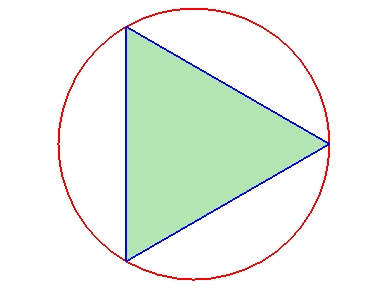
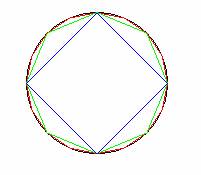
假定有兩個大小不同的圓 C₁ 和 C₂，其直徑分別為 d₁ 和 d₂、其周長分別為 l₁ 和 l₂。考慮這兩個圓的內接正 n 邊形 S_1,n  和 S_2,n，如下圖中的正四邊形、正八邊形或正十六邊形。

    

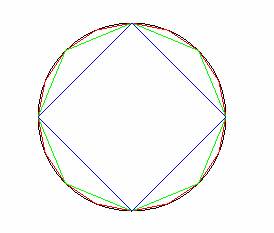
因為兩圓的內接正 n 邊形相似，所以其周長與圓的直徑之比相等；若 S_1,n  和 S_2,n 的周長分別為L_1,n  和 L_2,n，也就是說

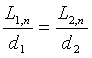
當邊數 n“愈來愈大”時，正 n 邊形就會“ 變成 ”圓，而 L_1,n  和 L_2,n 就會分別“ 變成 ”l₁ 和 l₂；所以

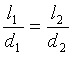
換句話說，就是圓周長與直徑之比會相等。
　

這不但說明了圓周長與直徑之比為定值－圓周率，也提供了一個估算圓周率的方法。若以圓的內接正六邊形的周長來估計圓周，如下圖：

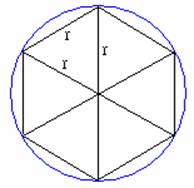
我們都知道圓的內接正六邊形的邊長等於圓的半徑；因此，內接正六邊形的周長（6r）為直徑（2r）的 3 倍，於是我們得到 π（圓周長與直徑之比）的值大約是  3。顯然圓周長比內接正六邊形的周長大，因此 π 會比 3 大一些！事實上，任何圓的內接正多邊形的周長都比圓周小。因此，若以圓的內接正多邊形來估計圓周率都會比正確的圓周率小一些。
　

換個角度來看，當 n（n 為正整數）“很大”時，圓的外切正 n 邊形也“幾乎”是圓。我們也可以用圓的外切正 n 邊形來得到圓周率的估計值。因為圓的外切正 n 邊形的周長都比圓周大，若以圓的外切正多邊形來估計圓周率都會比正確的圓周率大一些。
　

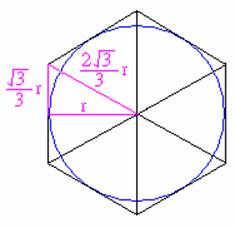
        若考慮圓的外切正六邊形，正六邊形可以分成 6 個正三角形，每個正三角形又可分成 2 個直角三角形，如上圖的紫色三角形。由於這種三角形有特殊的邊長比「1：2：」，而其中一邊又等於圓的半徑 r，所以按比例三邊長分別為 , , 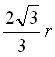r。於是我們可以算出外切正六邊形的周長為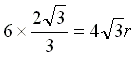，則

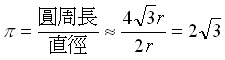  （實際上比要小一點）。

又因為 < 1.8（(1.8)²  > 3），我們知道 π 最大不會超過 3.6。
　

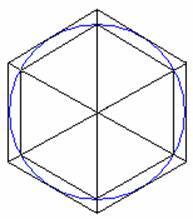
        顯然圓周長會介於圓內接正六邊形與圓外切正六邊形的周長之間，我們也因此可以得到 π 是介於 3 與 3.6 之間。

一如上述的方法，我們若同時以圓的內接及外切正多邊形來估計圓周率，我們便能知道估計值的精確性。