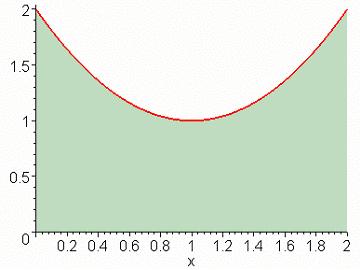
積分問題的起源即是求面積的問題，基本概念十分類似阿基米德的窮盡法。如下圖所示，我們想要求出由紅色函數圖形、x 軸、x = 0 與 x = 2 所圍出區域的面積。
首先將
0
到 2
的區間分割成 n
個子區間，左圖長方形的高度為該子區間函數的最小值，所以長方形的面積總和必小於所求之面積。相反地，右圖長方形的高度則為子區間內函數的最大值，所以長方形面積的總和也會大於所求之面積。隨著
n 越來越大，左圖長方形面積的總和
L
會越來越大，而右圖長方形面積總和 U
會越來越小，兩者之間的差 E
會趨近零。也就是說，兩者會同時趨近所求的區域面積。
|
|
|
|
|
|
這些長方形的面積總和的極限便稱為 f
在 [a, b] 上的積分，記做
。
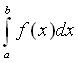考慮一個簡單的函數
f (x) = x，
的值是多少呢？
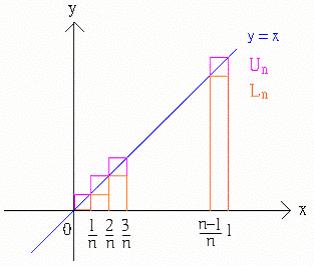
由上圖，我們可以看出
當
n 愈來愈大時，
愈來愈接近零，所以
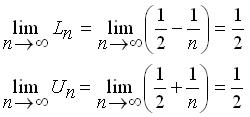
因此
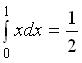
可以想像，如果我們要以類似的方法求
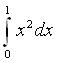(或是
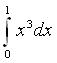)，那就得計算
（或是
），這可是件十分令人頭痛的事！這也難怪積分的概念
在微分之前很早就就已產生，但在微積分基本定理出現之前卻沒有什麼進展。
微積分基本定理
微分的技巧在牛頓及萊布尼茲手中得到了有系統的發展，他們建立了一些很有用的公式，使微分的運算變得容易。不僅如此，更重要的是，他們認識到微分和積分這兩種表面上看起來毫不相關的極限之間的密切關係而得到了「微積分基本定理」。
假設
為連續函數，
(i)
若對所有的
，令
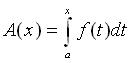，則 
。
(ii)
若對所有的
，
，則
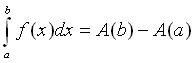
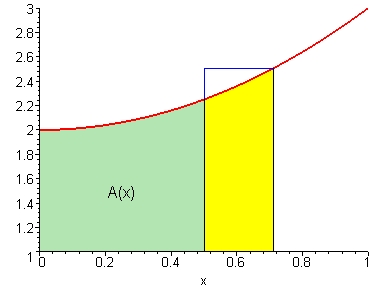
直觀地看，動畫中黃色的面積為 A(x+h) - A(x)；當 h 很小的時候，
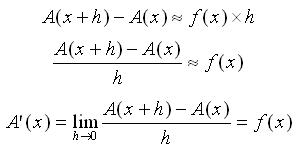
之前我們看到即使很簡單的函數，直接由定義求定積分也大都是很困難的事；有了微積分基本定理，積分就變成了微分的反運算，微積分學因而有了革命性的突破。
例如：若 n 為自然數，因為
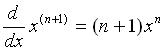
所以
。
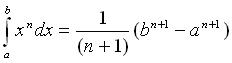