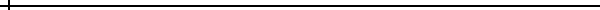
一般人常認為數學中充滿了數,也充滿了“公式”。沒錯,在數學中我們希望找到適當的“公式”來描述狀態或現象。
以圓來說吧!所謂圓就是平面上所有到某定點(圓心)距離為某固定數(半徑)的點所成的集合。由畢氏定理得知平面上兩點
(x0, y0), (x1, y1)
的距離為
![]() 。
。
而既然圓上的點 (x, y) 與圓心 (x0, y0) 的距離就是半徑 r,即
![]()
將等式兩邊一起平方,便得出了圓的“公式”:
(x – x0)2 + (y – y0)2 = r2
然而描述這類“公式”的工具,是數學上所稱的函數(function)。因此,我們在介紹微積分之前得先說說什麼是函數。
什麼是函數?函數就好像一個魔術師的戲法箱,只要給適當“輸入”就一定會有“輸出”,而且相同的輸入必定會得到相同的輸出。
![]()
舉例來說:若車速固定為
![]() (等速運動),
(等速運動),
1 分鐘後,車子行駛的距離為 1.5 公里。
2 分鐘後,車子行駛的距離為 3 公里。
3 分鐘後,車子行駛的距離為 4.5 公里。
4 分鐘後,車子行駛的距離為 6 公里。
:
:
其實,由“公式”
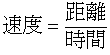
我們知道
t 分鐘後車子行駛的距離為
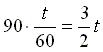 公里。
公里。
如此,我們輸入的值是車子行駛的時間,輸出的值是車子行駛的距離,我們就得到一個函數描述該車的行駛狀況。
![]()
在上例中,我們通常以符號
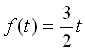 來表示這個距離函數。其中
f 是函數的名稱(當然不一定要叫
f,也可以取其他的名字),小括號裡面放的是輸入的時間,等式右邊則是輸出的距離。
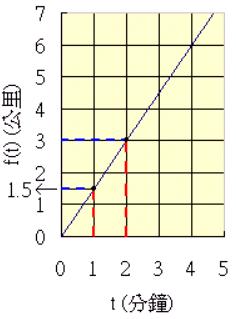
這個函數也可以用平面圖形來表示:橫座標為輸入值,縱座標為輸出值。
來表示這個距離函數。其中
f 是函數的名稱(當然不一定要叫
f,也可以取其他的名字),小括號裡面放的是輸入的時間,等式右邊則是輸出的距離。
這個函數也可以用平面圖形來表示:橫座標為輸入值,縱座標為輸出值。
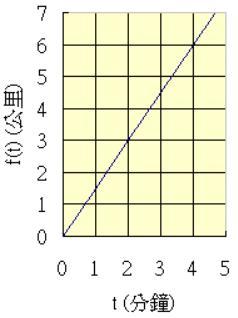
由這個函數圖形我們可以看出當輸入值為 1 分鐘時,輸出值對應到 1.5 公里;而輸入值為 2 分鐘時,輸出值則對應至 3 公里。
函數觀念的產生使數字能夠描述“運動”或動態的事物。再看看另一個等速度運動的例子,若車速固定為
![]() ,則會得到距離函數
,則會得到距離函數
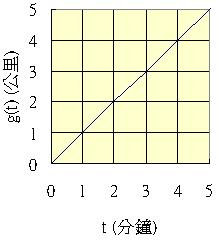
g(t) = t(t的單位為分鐘)
它的函數圖形如下:
如果行車速度固定為每小時
v0
公里,距離函數則為
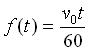 公里(t 以分鐘為單位),函數圖形都會是一條直線。而且這條直線的斜率為
公里(t 以分鐘為單位),函數圖形都會是一條直線。而且這條直線的斜率為
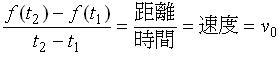
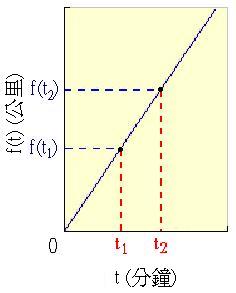
換個角度想,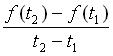 可以說是
f (t)
從
t2
到 t1
之間的平均速度,也就是平均變化率。因為這裡的運動為等速度,所以每一瞬間的速度也等於平均速度。
可以說是
f (t)
從
t2
到 t1
之間的平均速度,也就是平均變化率。因為這裡的運動為等速度,所以每一瞬間的速度也等於平均速度。
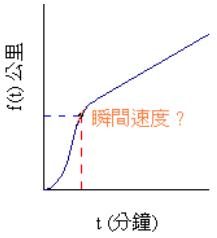
然而,我們常常會遇到非等速運動,其函數圖形無法以一條直線來表示,如下圖,那麼對於這樣的函數,我們有辦法知道每一刻的“瞬間速度”嗎?