1  2  3  4  5  6  7  8  9   Contents

極限

        一個函數 f (x) 當 x 趨近 a 的極限為 L，記做 ，意思是：

「當 x 夠靠近 a 時，f (x) 和 L 的距離（也就是 | f (x) – L | ）要有多小就有多小。」

怎麼說「要有多小就有多小」呢？也就是說任給一個距離（正數 ε），我們總可以找到一個距離（另一個正數 δ），只要 x 和 a 的距離小於 δ 但 x ≠ a 時，f (x) 和 L 的距離就會小於 ε；換句話說，只要 0 < | x – a | < δ，我們就能保證 | f (x) – L | < ε。

（ε (epsilon)，δ (delta) 這兩個希臘字母數學上通常代表很小的數。） 

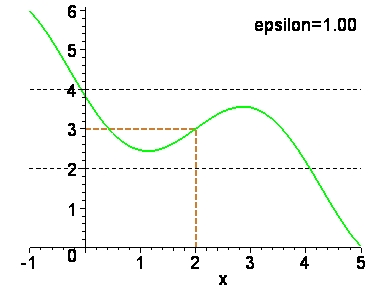
以下面的動畫為例：

給定的距離（ε）為 1 時，我們可取 δ 為1。
給定的距離（ε）為 0.8 時，我們可取 δ 為 0.8。
給定的距離（ε）為 0.6 時，我們可取 δ 為 0.6。
給定的距離（ε）為 0.4 時，我們可取 δ 為 0.4。
給定的距離（ε）為 0.2 時，我們可取 δ 為 0.2。
　

 

 

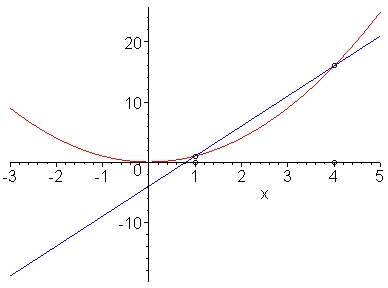
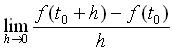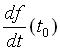        若極限 存在，則我們說 f 在 t₀ 的微分（或導數）存在，記做 f '(t₀) 或 。以圖形的角度來看，f '(t₀) 則是函數圖形在 t₀ 點的切線斜率。如果 f 為描述運動的距離函數，f '(t₀) 就表示此運動在 t₀ 的瞬間速度；一般的情形，f '(t₀)表示 f在 t₀ 的瞬間變化率。