1  2  3  4  5  6  7  8  9   Contents

瞬間變化率及微分 

        假設行車距離是一個時間函數  f : [ a, b ]→R，而 t₀ 是（a, b）中的一個點（數）。

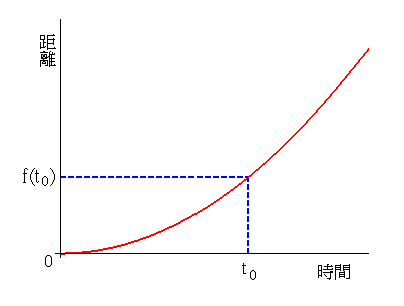
之前我們談過 （t₀ , f ( t₀ )）和 （t₀ + h , f ( t₀ + h )）這兩點連線的斜率

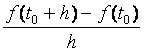
表示從 t₀ 到 t₀ + h 之間的平均速度。

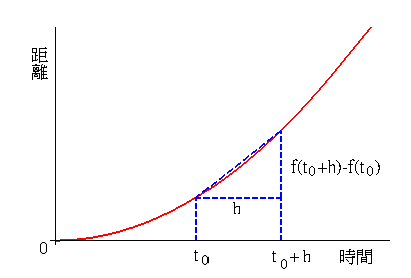
若 h 愈來愈小，則函數 f 在 t₀ 附近的的行為則愈來愈類似等速運動，而（t₀ , f ( t₀ )）和（t₀ + h , f ( t₀ + h )）這兩點連線的斜率便愈來愈接近車子在 t₀ 的“瞬間速度”。

     

　

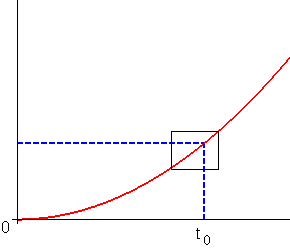
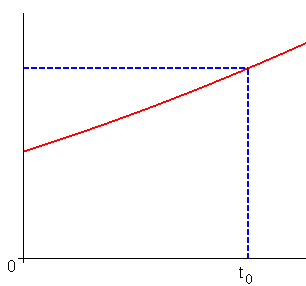
        如果距離函數為 f (t) = t ²，牛頓的方法是： 

首先讓 t₀ 漸漸增加到 t₀ + o，那麼 f  的值也會跟著由 t₀ ² 變成 (t₀ + o)²。所以在這兩點間的變化率就是

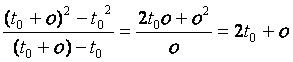
若我們盡可能取到很小很小的 o，讓它近乎於 0 （但又不能為 0），那麼在 t₀ 的“瞬間速度”就可以看成是 2 t₀ + 0 = 2 t₀。
　

        牛頓的方法也可以應用到其他像 f (t) = t ³ 的函數；萊布尼茲也用類似的手法，不同的是他用 dt 來表示“極小的 t 值”，而不是 o。

        然而，“很小很小”是多小？ 毫米夠不夠小？毫微米夠不夠小？奈米呢？